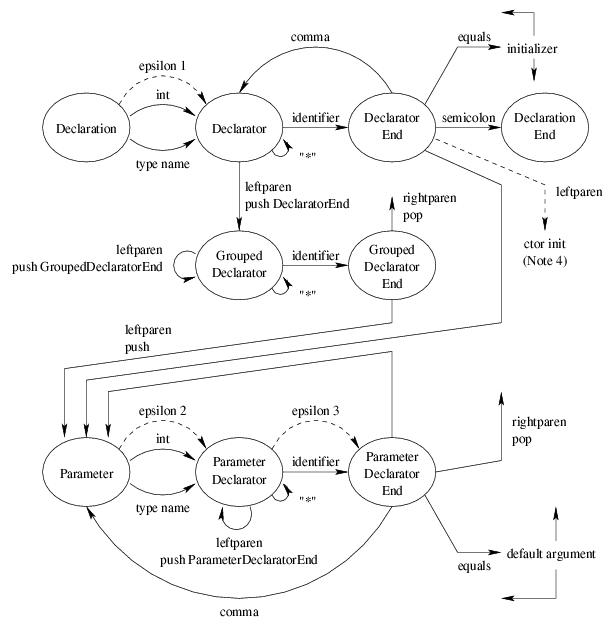
One of the trickier aspects of parsing C and C++ is parsing the declarator structure. In cc.ast.html, I showed a diagram of how a somewhat complicated declarator is to be decomposed; but there is no suggestion there of how that decomposition is accomplished. The mechanism of said decomposition, namely parsing a declarator, is the subject of this document.
The parsing algorithm can be succinctly described by the following
pushdown automaton:

Quick pushdown automaton refresher: A pushdown automaton is like a finite automaton, transitioning from state to state as it consumes input. In addition, it has the option of pushing a state onto its pushdown stack while making a transition, or popping a state off the stack instead of making a fixed transition. In the diagram above, every transition on "leftparen" is accompanied by pushing a state (if I don't say which state, it means push the state you just came from), and every action on "rightparen" is to pop a state (and go there). As demonstrated by this example, a pushdown automaton is more powerful than a finite automaton in that it can deal with arbitrarily nested constructs.
Ignoring the dashed arrows (which are discussed below), this automaton is completely deterministic: in every state, for every next token, there is either zero or one possible transitions (zero transitions corresponds to a syntax error). This deterministic automaton is the core of the declarator parser mechanism.
Note that the automaton only includes the pointer type constructor "*" and function type constructor "()". I have left out references ("&"), arrays ("[]"), and pointer to member ("class::*") for simplicity. I have also left out the possibility of a parameter list being empty; adding it is a matter of splitting "Parameter" into "FirstParameter" (rightparen enabled) and "NextParameter" (reached by comma; rightparen not enabled), but I decided it's more clutter than it's worth here.
From here, I will consider in turn three complications that Elsa must deal with.
Parameters do not have to be given names; it is sufficient to give their types, for example:
int strcmp(char*, char*);
The effect on the automaton is to introduce an "epsilon transition", that is a transition that does not consume any input. In particular, it introduces the transition from "Parameter Declarator" (PD) to "Parameter Declarator End" (PDE), labeled "epsilon 3". Equivalently, all of the outgoing transitions for PDE are available in PD.
However, this creates a non-determinism: both PD and PDE have an outgoing transition on leftparen, and they do not go to the same place. This choice, between "(" as a grouping punctuator and "(" as the function type constructor, is resolved in the C++ standard (section 8.2 paragraph 7, plus some deduction) by looking at the token after the "(" in question. If it is a type keyword, or an identifier that names a type (in the current scope), or a rightparen, then the function type constructor interpretation is preferred. Otherwise, the grouping punctuator interpretation is used. Example:
int f( int (int) ); // 'f' accepts (a pointer to) a function typedef int x; int f( int (x) ); // same type as above int g( int (y) ); // 'g' accepts an integer int h( int () ); // 'h' accepts a function
In C++, objects can be initialized by invoking a constructor ("ctor"):
class A {
public:
A(int, float);
};
A a(3, 4.5); // initialization by ctor call
In the automaton, this possibility adds an transition on "leftparen" from "Declarator End" (DE) to the parsing of an argument list (not shown); the arc is labeled "ctor init (Note 4)" (CI).
Unfortunately, there is already a transition on "leftparen" in that state, to "Parameter" (P). How do we decide whether to go to P or CI? The C++ standard (section 8.2 paragraph 1) says that if a construct "could possibly be a declaration" then it is a declaration. What this (apparently) means is that we prefer the P interpretation, as that entails parsing a parameter declaration, instead of the CI interpretation. But exactly what circumstances are covered by the phrase "could possibly be"? How much checking should be done before deciding whether something could be a P; must we go all the way to type checking?
Now, in fact, Elsa does go all the way to type checking, though that's an artifact of what is convenient in Elsa, not a determination of what is perfect behavior (see below). For this document, I want to have a simple, local rule. As best I can tell, the determining factor is again the token after the "(": if it is a type keyword or an identifier that names a type, choose P, otherwise choose CI.
In old-style Kernighan and Ritchie (K&R) C, declarations were allowed to omit specifying the type of a declared variable, and the type would implicitly be "int". C++ does not allow this, but Elsa (in certain configurations) nevertheless allows this rule. In the automaton diagram, this adds the epsilon transitions labeled "epsilon 1" and "epsilon 2".
Transition "epsilon 1" is easy to handle. It adds no nondeterminisms.
Transition "epsilon 2" is more interesting. It creates a nondeterminism for an identifier that names a type, since P can transition to PD or to PDE (using the implicit int for the latter). However this is a familiar ambiguity for implicit int, and is resolved in the usual way: prefer the "type name" interpretation.
Interestingly, gcc (which is for the moment my only reference for what K&R is) does not accept arbitrary use of implicit int for parameters. Instead, it only allows it when the "register" keyword is used. Thus, "epsilon 2" is really only available when that keyword appears first (the automaton does not include such keywords, for simplicity). Elsa doesn't enforce this.
Now, the fact is that Elsa does not use a directly-written pushdown automaton to parse declarators, but a grammar instead. Morever, that grammar was designed before the automaton was conceived (the grammar is based on the grammar in the C++ standard). So what role does the automaton play?
Bascially, I use the automaton as a conceptual tool, to let me analyze tricky example syntax to figure out the "right" behavior. Then, I modify the grammar and/or type checker to get the behavior I want.
It's somewhat ironic that my specification is the low-level automaton, and my implementation is the high-level grammar. However, this is due to the fact that C's declarator parsing rules were developed along with other low-level implementations, so those rules are easier to formulate as low-level rules. Fortunately, this is the only part of the language that has this specification inversion property; for all other parts, the high-level grammar spec is much preferable to an automaton.
As hinted above, Elsa resolves ambiguities during type checking, rather than during parsing. This is because Elsa does not use the "lexer hack" feedback technique, and hence does not have enough information at parse time to do ambiguity resolution.
The particular strategy employed is typically to type check both alternatives of a given ambigutiy, and keep the one that checks without any errors. In the case of the declarator ambiguity, Elsa checks the declarator possibility first, and keeps it if it succeeds, regardless of what might happen to the other alternative.
This strategy works well when the input is assumed to be valid C++. However, there is a risk that Elsa will accept code that is not valid C++, if: